long division essay

So Long, Long Division

• Share article

With the possible exception of fractions, no elementary math topic or skill stresses students out more than long division does. And it’s so unnecessary--not just the stress, but the skill. Think about it. How often do you use long division? For that matter, how often do mathematicians use it?

When I observe classes where students are working on long division, there are always a few kids who have the routine down and get one correct answer after another. No stress for these students because they’re feeling successful. But ask them what they’re doing, and they’re likely to refer to a mnemonic like “dad, mom, sister, brother” (divide, multiply, subtract, bring down). Ask them how they knew where to place the two numbers, and they’ll tell you “the bigger one always goes inside the house.” These students can do division, but do they understand division? And how’s their number sense?

Then there are those students who not only don’t get division but also can’t do it. Some of these students avoid long division problems by disrupting class, going to the bathroom, or putting their heads down. But other students try and try and try. And they fail and fail and fail. On the one hand, it’s great that they’re persistent, since we want students to engage in productive struggle. We also want them to make sense of problems and persevere in solving them, per Practice Standard #1 of the Common Core State Standards (see my last post, Engaging Math Students in Productive Struggle ).

Long division, however, isn’t a problem-solving exercise for students. It’s a procedural exercise. And if a procedure doesn’t make sense for them or they lack the skill to be successful with it, they’re not engaged in productive struggle. They’re engaged in unproductive suffering.

I’m reminded of a student who was grimacing as he stared at a problem for a few minutes, pencil in hand but nothing on his paper. I approached him and noticed the problem he was stressing over was 700 ÷ 20. After a few words of comfort, I said what I often say to math students: “please put your pencil (or pen) down, and look at me.” I then asked him, “What’s 100 divided by 20?”

“Five,” he said without hesitation, and then picked up his pencil and wrote seven 5s in a column on his paper. He then counted by fives, and wrote 35 as his answer. And he was grinning rather than grimacing.

So, who understands division better: the arithmetically challenged student in this example or a student who gets the right answers with the aid of a mnemonic? Of course kids need to master division in order to be successful in math. But instruction that focuses on procedures helps some students do math, while helping few students know math.

A better approach is to advise students to put their pens and pencils down (calculators too), and estimate quotients before trying to compute them. Estimation before computation is an important first step in the problem solving process for a few reasons: it compels students to read and think about what’s being asked in a problem; it helps students develop number sense; and it gives students ballpark answers to compare their precise answers with, prompting them to reconcile any significant differences. What’s more, estimation is a far more practical skill--for math and life--than paper and pencil computation.

After students have estimated, ask them to keep their pencils down and identify the most efficient strategy for a given problem. Encourage them to use mental math or play around with the divisor or dividend to make a problem more manageable, as in the example above where I asked the student, “What’s 100 divided by 20?” Pushing students to think before resorting to a procedural approach (or reaching for a calculator) helps deepen their conceptual understanding. It also creates opportunities for them to learn other math concepts/skills. (I just worked with another arithmetically challenged student who discovered the distributive property after breaking a dividend up into the sum of two numbers.)

What do you think? Am I missing something here? Do you have a good reason for students to learn long division that I’m overlooking? If not, please join me in saying “so long” to long division.

Image provided by GECC, LLC with permission

The opinions expressed in Coach G’s Teaching Tips are strictly those of the author(s) and do not reflect the opinions or endorsement of Editorial Projects in Education, or any of its publications.

Sign Up for EdWeek Update

Long division

How Can Help Students Acquire Proficiency With Long Division?

create challenges that expose students to build on patterns and number sense. Division is no exception; students should be able to make connections to place value, patterns, and previously used strategies to solve division problems. Therefore, once students reach a certain point of fact fluency they must develop new methods to perform divisions. As explained in the Inside Division video, (Laureate, 2013) when solving division problems with higher dividends some strategies are no longer practical. The

The Cover Of Long Division

The cover of Long Division, by Kiese Laymon, pictures a rusted, broken chain. This symbol, along with the setting of the book suggests the strong history of slavery in the South. That unfortunate history carries with it the idea of otherness—an idea of being valued and devalued based on skin color – an idea central to Laymon’s story. Long Division shows throughout three time periods that while the African American race progresses, it never arrives at full equality. In each time period — 1964, 1985

Long Division Research Paper

Learning Long Division A time I struggled in my life was when I had to learn long division. It happened while I was in the fourth grade; I just couldn’t catch on and was quickly becoming frustrated. Math had always been one of my weakest subjects. Then one Sunday afternoon, my mom made me sit down and helped me learn it. To make matters worse, it was a beautiful early spring day. The sun was shining brightly outside, and I could hear the “pop” of baseballs hitting gloves as my buddies

Analysis Of The Book ' Long Division ' Essay

The topics “Can You Use that Word in a Sentence,” and Racial Representation is significant throughout the book Long Division written by Kiese Laymon. The characters in this book will have to face racism and learn to defy racial representations, especially during the scene of the quiz contest. Overall, this essay will tackle the importance of language in the book Long Division and analyze the actions of the characters and the emotions they display. This essay will examine the words written and the

Long Division, The Ideal Man Essay

person, generally black men all are bound to the same rules. Ralph Ellison’s novel Invisible Man explores the intersections of race and power, where this seemingly ideal black male is one that can outwit the white men. In Kiese Laymon’s novel Long Division, the ideal man is one that can survive white oppression by not coinciding with racial stereotypes. Although these novels introduce the same idea of the us-versus-them mentality, both have vastly differently interpretations on it and ways of fulfilling

The Teacher Had Put On Board

“Slightly and squeaky!” The door to the classroom flew open as I burst into the room and sat in my usual seat. This was the day I was going to learn how to do polynomial long division. “Good morning.” The professor said, as she walked into the classroom. Almost every one of the students had at least a pencil and notebook, copying notes that the teacher had put on the board. After writing the notes down, I said to myself, let me try to do one of the problems that the teacher had put on board. Surprisingly

Cindy The Clover: A Short Story

Cindy the Clover: “Good morning class let’s open our books to page- The door quickly slams open, and a small spiky figure is seen hurrying to a forgotten desk in the back of the room. Cindy the Clover: “Barbara Rose!” she said angrily “What is the meaning of this?” “Is there a reason why you are late to class for the fourth time this week?”Barbara hung her bud, down over her desk in shame and meekly replied “I’m sorry Mrs. Clover, I didn’t mean to be late again, it’s just I live so far away, and

‘’Slightly and squeaky!” The door to the classroom flew open as I burst into the room and sat in my usual seat. This was the day I was going to learn how to do polynomial long division. “Good morning.” The professor said, as she walked into the classroom. Almost every one of the students had at least a pencil and notebook copying notes that the teacher had put on the board. After writing the notes down, I said to myself let me try to do one of the problems that the teacher had put on board. Surprisingly

Hrm/531 Week 2 Assignment

as a three-day unit focusing on long division by modeling division with place-value blocks, dividing 2-digit by 1-digit numbers, and dividing 3-digit by 1-digit numbers. Students were introduced to division prior to my learning segment but the struggled to understand and comprehend division because students were only introduced to the division algorithm and were not provided with a mnemonic to help them recall the steps. Students also weren’t introduced to division with manipulatives or drawings.

British Airways Case Summary

They should start the change in some of their more profitable divisions of the company. They have proved that they are profitable so they have the human resources, marketing and finance divisions’ in-line. They would need to have someone in to teach them about the port-of-entry division to make them a solid solo division that is completely decentralized from TMC. From there they would need to monitor the division to see where any possible issues may occur and iron them out. From there

Popular Topics

• Timing belt
• Roman commerce
• Rafael Nadal
• DNA vaccination
• Continuous integration
• Saint Timothy
• Baritone saxophone
• University of Western Australia
• Braille music
• Braille code

Long Division Algorithm

1.2 Background to the problem Learners are exposed to different kinds of methods when dividing numbers for example using the invented method, but however long division is regarded as the standard algorithm or traditional algorithm when dividing numbers in mathematics (Beckmann. 2011). When I was teaching this particular topic of long division in mathematics and what I had observed in school environment learners mostly complain, moreover claim not to understand how the long division standard algorithm works when they are busy with dividing numbers and asked to divide more than two digit numbers. This topic takes up much of the time for learners to master the concept of division using the standard algorithm. I spent more time teaching long …show more content…

What approaches do teachers use to teach long division method? What are the reactions of the learners? What prevents learners understanding the concept of long division? Which approaches can be used to teach long division to make learners understand? How can the learners follow the correct steps to use long division? What difficulties learners experience with long division? 1.4 Significance of the study The main aim of the study is to make teachers aware why learners find it difficult to learn long division and how to teach long division. It will also assist teachers to use different approaches to teach the standard algorithm that will promote understanding among learners. Teachers will be guided to discover learners’ weakness when using the long division standard algorithm when solving division problems. 1.5 Limitations Initially there is not much report on why it is difficult for learners to learn how to use long division standard algorithm to divide numbers, and how teachers can teach long division to make learners …show more content…

It has been found however that several students struggle to use the algorithm correctly, and those who do, many perform the correct steps without relating the taught procedure to the concept of division or their daily experiences of sharing and grouping” (P.1827). In the Namibian concepts this particular method is also used in schools when learners are being taught division in mathematics, most specifically when dividing a four digit number by a two digit number it will be conveniently use long division method to get the correct answer to find either the quotient or the

Nt1210 Unit 12

Children in this group were provided with base-10 and unit blocks. Each base 10 block is 1 cm × 1 cm × 10 cm in size. Each unit block is 1 cm × 1 cm × 1 cm in size. The research assistant gave explicit demonstrations of how to use both base-10 block and unit blocks to construct two-digit number. First, the research assistant placed out ten unit-blocks in a line and then put a base-10 block along to the ten unit-blocks.

Nt1310 Unit 1 Activity 2

From the idea that they know that $x^2 - x$ is equal to $x(x-1)$, I was able to help to construct that knowledge. I also realize that complicated problems are always stressing the child, for this reason, we must first help them to solve the easy problem, once they are familiar with them then we can include the complicated ones. Cooperative learning promotes a positive relationship and communication

Nt1310 Unit 8 Assignment 1

Today, I want to teach you another way or a shortcut (algorithm) to solve three-digit number subtraction problems. Guiding Question Description for Students of Expected

Mat 540 Week 4 Assignment

During the last 50 hours, Ashley has been working on learning the division facts and has learned to multiply 2 and 3 digit numbers by 1 digit with all combinations of regrouping. In both these areas she has built fluency. She moves through problems quickly with very few errors. The third grade standard is to be able to multiply and divide within 100. Ashley is currently multiplying within 1000.

Wgu Math Task 1

In Math, Scott is working on developing a strategy to help him solve one-digit and two-digit multiplication problems. He has been exposed to the Bow-Tie method for two-digit, grouping and the array strategy for one-digit multiplication. He is doing very well at understanding and using the method to assist him in solving the multiplication problems. There have been improvements in his assessments by creating a strategy that works for him. After Scott has used the strategy over time, he will develop automaticity for solving the multiplication.

Video Analysis: The Power Of 2 By Marilyn Friend

Overall, the fundamental approaches shown in the video can provide educators with valuable data which can guide instructional procedures in the classroom. One approach shown in the video is station teaching. In this strategy students are divided into small groups and placed into stations. By using groups teachers can focus on different aspects of the curriculum, which builds upon previously learned material. In addition, station teaching breaks the traditional cycle of large group instruction and allows students to receive individualized attention.

13 Rules That Expire Summary

Math is often one of the hardest subjects to learn. Teachers know rules that can help students, but often they forget that those rules become more nuanced than presented.

Summary Of Never Say Anything A Kid Can Say Reinhart

Reinhart explained that through a normal teaching method, the teacher presents information to the class through explanations and some demonstrations. Through this process, the teacher must first

Ofsted's 'Made To Measure'

Ofsted’s 2012 report ‘Made to Measure’ states that even though manipulatives are being utilized in schools, they aren’t being used as effectively as they should be in order to support the teaching and learning of mathematical concepts. Black, J (2013) suggests this is because manipulatives are being applied to certain concepts of mathematics which teachers believe best aid in the understanding of a concept. Therefore, students may not be able to make sense of the manipulatives according to their own understanding of the relation between the manipulative and concept. Whilst both Black, J (2013) and Drews, D (2007) support the contention that student’s need to understand the connections between the practical apparatus and the concept, Drews,

Standardized Education In Charles Baxter's 'Gryphon'

This quote proves the interest the children having in learning about these things. Rarely do fourth graders happily discuss arithmetic to any extent. Miss Ferenczi is a positive influence by teaching them to be excited about learning through the stories she tells them.

Two Critical Elements Of Instructional Scaffolding

I would constantly refer to both the mnemonic device and guided examples as I verbalized the task. Sixth, I would also use modelling and practice to help my student understand the patterns in solving long division, and support his or her confidence in his or he ability to perform and complete the individual steps of long

Plane Crash Theory

The first example he gives demonstrates the ability of math, contrasting Western students and Asian students. The number-naming systems in Western and Asian languages are completely different. The number system in Asia is logical and the words are brief, allowing more numbers to be memorized and recalled. The opposite is true for the system in Western society. This difference allows Asian children to learn numbers much faster than American children.

Four Major Theories Of Human Development

Introduction It is very important to study about the development of the human. Because it provides framework to think about human growth, their mental development, and the most important one, ‘their learning’. As a teacher it is very important to study about these theories. Because it have a close relationship with the development of the students and their learning behavior (Michael, 2012) .

Benefits Of Dialogic Teaching

Those five ways include i) whole class teaching, ii) group work (teacher-led), iii) group work (student-led), iv) one-to-one (teacher and student) and v) one-to-one (student pairs). Whole class teaching seems to be the most important way in my class and I can be very sure in any other class since it is the main method uses to convey knowledge to students. Students get very comfortable and happy doing group work but there is a little case in which student is prefer to do individual work. No matter which way is selected, indirectly, students are actually developing their critical thinking. It is proved when students submit their work or project.

Benefits Of Direct Instruction

It is a very common teaching strategy, relying on strict lesson plans and lectures with little or no room for variation. Direct instruction does not include activities like discussion, recitation, seminars, workshops, case studies, or internships. DI is probably the most popular teaching strategy that is used by teachers to facilitate learning. It is teacher directed and follows a definite structure with specific steps to guide pupils toward achieving clearly defined learning outcomes. The teacher maintains the locus of control over the instructional process and monitors pupils ' learning throughout the process.

More about Long Division Algorithm

Related topics.

• Mathematics
• High school

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

How to do long division

Statistical model analysis (math 341), depauw university.

Students also viewed

• Peacebuilding relection
• Sample Case Study 2 - n/a
• Cervantes. humane immigration enforcement
• A Streetcar Named Desire, by Tennessee Williams
• Corp.Kahan - Derperlfja;dfka;fdk
• Criminal Law 2017 - final exam

Related documents

• Study Guide Quiz 1 - mmmmmmmmmmmmmmmm
• Exam 3 Mock Questions - mmmmmmmmmmmmmmmmmmm
• Case study-Antibiotic resistance
• Virus Presentation Rubric
• Wastewater Fieldtrip Worksheet
• David's Tewwg Class Essay

Preview text

How to do long division.

coolmath4kids/math-help/division/how-do-long-division

####### Let's just dive right in and do one! I'm going to go really slowly and I'll

####### show each step. After you see a few examples, it's going to start making

####### sense!

####### The first thing we do is change the way the problem is written...

####### The first math step is to look at that first number of the guy we are dividing

####### into... that 6. This is the division step!

####### We want to see how

####### many times 2 will go into 6 ... 2

####### goes into 6 three times, right?

####### So, we put that 3 right above

####### the 6 :

####### Here's the second step... This is the multiplication step!

####### Multiply the 3 and the 2 and

####### put the answer right under the

####### 6 :

####### Here's the third step... This is the subtraction step!

####### Do the subtraction...

That's 6 - 6 = 0

####### We just finished the first chunk of steps! And it wasn't that bad!

Division, then multiplication, then subtraction.

Let's call it the dms loop.

####### Those letters go alphabetically!! You can use that to remember it!

####### OK, now we're going to do the exact same thing, but with a different

####### number...

####### First thing:

Drag the 8 down.

####### Now, let's go back into our division, multiplication, subtraction loop using

####### the 8!

####### many times 2 will go into 8 ... 2

####### goes into 8 four times... So, we

####### put that 4 right above the 8:

Multiplication:

####### Multiply the 4 and the 2 and

####### 8 :

####### Here's another one:

####### Set it up:

####### Remember, the DMS loop! Division, then multiplication, then subtraction...

####### and we do this until we run out of numbers!

####### We want to see how many times 3 will go into 7 ...

####### Hmm... It doesn't go in cleanly does it? From our times tables, we know

####### that 3 goes into 6 and 3 goes into 9. But, 3 doesn't go into 7. That's OK.

####### So, what does 3 go into that's a little less than 7? SIX! Three goes into 6

####### two times.

####### So, 3 goes into 7 two times...

####### with a little left over. Put that 2

####### right above the 7 :

####### Multiply the 2 and the 3 and

####### 7 :

Subtraction:

Do the subtraction..., that's 7 - 6 = 1, we just finished the first chunk of steps and it wasn't that bad, division, multiplication, subtraction., now we're going to do the exact same thing, but with a different number..., the first thing is to set it up:, drag the 5 down., that makes it a 15..., now, let's go back into our dms loop using the 15, we want to see how, many times 3 will go into 15 ... 3, goes into 15 five times... so,, we put that 5 right above the 5:.

####### Long division with polynomials works the same way. You just have to deal

with x junk along the way.

####### Let's walk through one:

####### So, we are looking at

####### The easiest thing to do is to write it like

####### Now, do what you did with regular long division:

####### Before we go on, I want to point out something very important to you...

####### See these parentheses? If you don't put them in, you'll do the entire

####### problem WRONG! Why?

####### Because that minus distributes into the second guy!

####### Finish the subtraction!

####### Check it by multiplying!

####### Get out a piece of paper and work along with me on this!

Things to Watch out for

####### Here's one thing that can happen:

####### Look at this:

####### Whenever you set these guys up, you need two things:

####### We haven't changed his value... But, we've added some important place-

####### holders. I call them "dummy guys."

####### If you don't have the dummy guys in the setup, you're going to get stuck

####### with a situation that you don't know how to deal with...

####### Check it out:

####### Do the first chunk of the problem WITH the dummy guys:

####### If you didn't have the dummy guy:

####### Try working the rest of the problem the right way. I'll do it on the next page.

####### Let's try one:

####### Set it up and remember the dummy guy:

####### Start working it...

So, we stop here and the 40 is our remainder.

####### Here's the official answer:

• Multiple Choice

Course : Statistical Model Analysis (MATH 341)

University : depauw university.

Long Division – Definition, Steps, Method, Examples

Definition of long division, steps to carry out long division, fun facts about long division, solved examples on long division , practice problems on long division, frequently asked questions on long division.

In Math, l ong division is the mathematical method for dividing large numbers into smaller groups or parts. It helps to break down a problem into simple and easy steps . The long divisions have dividends, divisors, quotients , and remainders. In a long division problem, the dividend is the large number that is divided by another number called the divisor . The quotient is the result of the division, and the excess quantity that cannot be divided is called the remainder . 

Recommended Games

Example of Long Division 

Here is an example that will help us understand this concept:

As 75 is not a multiple of 4, it is not divisible by 4 and will leave a remainder at the end. 

Recommended Worksheets

More Worksheets

Symbol of Division

To show that two numbers are divided, we can add a division sign ‘÷’ between them. So, for example, if we have to show 36 divided by 6, we can write it as 36 ÷ 6. 

We can also show it in a fraction form as 366. 

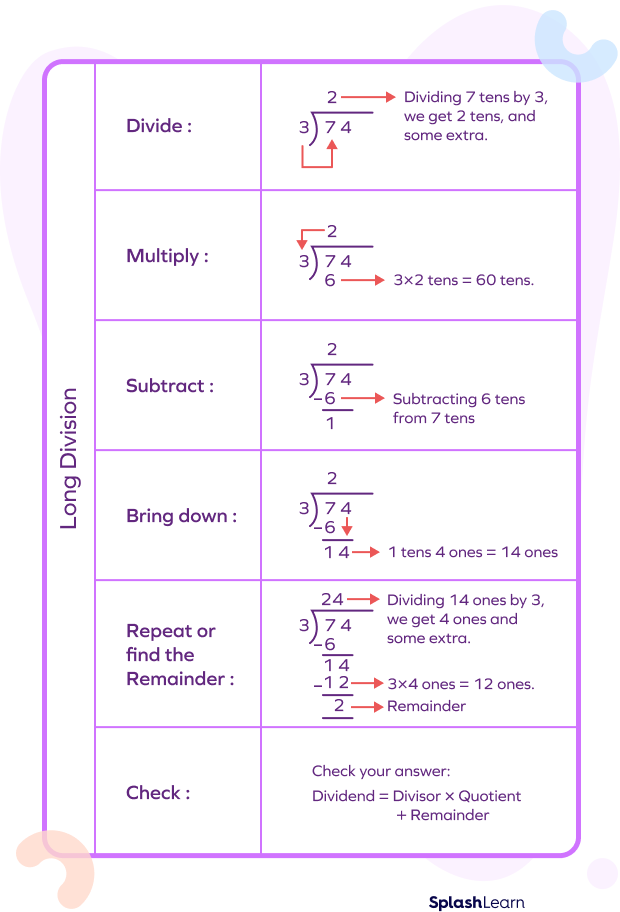
There are five steps to solve every long division problem with ease. 

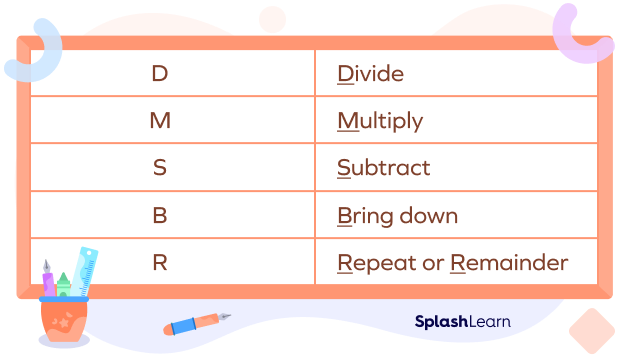
Let’s have a look at the examples given below for a better understanding of the concept.

Dividing Decimals Using A Long Division

Long division can also be used to divide decimal numbers into equal groups . It follows the same steps as that of long division, namely, – divide, multiply, subtract , bring down and repeat or find the remainder. 

Here’s an example of long division with decimals .

• If the dividend is 0, the quotient will always be zero.
• The remainder is always less than the divisor.
• Multiplying the quotient with the divisor and adding the remainder will give the dividend. 

(Divisor x Quotient) + Remainder = Dividend 

• When the remainder is 0, the dividend is the product of divisor and quotient.

Divisor x Quotient = Dividend, when remainder = 0

Long Division is an instrument that allows you to divide large numbers into multiple smaller groups or parts. When we divide a dividend with a divisor, the quotient obtained is the number of groups that can be made, and the remainder identifies how many elements or numbers that will be left ungrouped. To understand this concept even better, check out the wide range of interesting exercises available on SplashLearn and become a long division wiz! 

Question 1:  Divide 726 by 4  

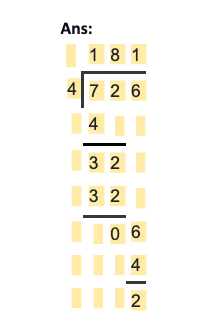
Hence, the quotient of the problem is 181, and the remainder is 2.

Question 2: What is the remainder when we divide 248 by 8?

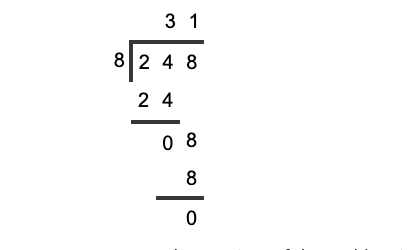
Hence, the quotient of the problem is 31, and the remainder is 0. 

Question 3: Laila’s mother collected all family pictures and wanted to place all of them in an album. If each page of an album can contain 9 pictures, how many pages of the album will she need if there are 285 pictures?

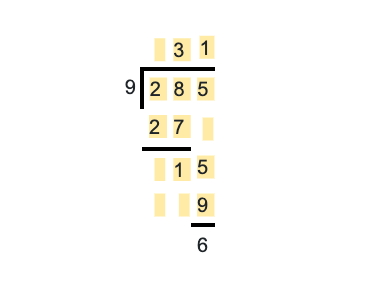
The quotient of the problem is 31, and the remainder is 6. So, she needs 31 + 1 (for the remaining six pictures) or 32 pages. 

Long Division

Attend this Quiz & Test your knowledge.

On dividing 426 by 4, we get the remainder as

Find the dividend if the divisor is 8, quotient is 71 and remainder is 4., find the digit that can replace a in the following division problem..

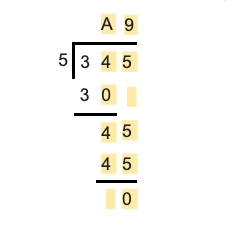
Can the divisor be 0?

No, division by 0 is not defined in Math generally.

What is the Long Division Method?

In Math, long division is the mathematical method for dividing large numbers into multiple smaller groups or parts. The number which we divide into small groups is called the dividend, the number by which we divide is called the divisor. It helps to break down a problem into simple and easy steps. 

How can we verify the quotient and remainder of a division problem?

​​We can verify the quotient and the remainder of the division using the division formula : (Divisor x Quotient) + Remainder = Dividend 

What is the difference between long division and short division?

The short division is great for dividing larger numbers by one-digit numbers, whereas the long division is handy for dividing large numbers by numbers with two or more digits. 

RELATED POSTS

• Quotient – Definition with Examples
• Commutative Property of Addition – Definition with Examples
• Seconds to Minutes Conversion
• Volume of Cuboid – Definition, Formula, Derivation, Examples, FAQs
• Simple equations and Application – Methods, Examples, Facts, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Understanding multiplication

Understanding division

Long division

Here you will learn about long division, including how to divide using long division and solving for quotients with and without remainders.

Students will first learn about long division as part of the number system in grade 6 and will continue to use the skill throughout middle school and high school.

What is long division?

Long division , also known as the standard algorithm, is a standardized process used to divide multi-digit numbers, by breaking the multiplication into a sequence of steps.

Before performing long division, you must first understand the different parts of a division equation:

• The dividend is the number that is being divided equally.
• The divisor is the number that divides the dividend. It is also thought of as the number of items in each group, or the number of groups.
• The quotient is the answer of the division process. In some cases, there may be a remainder included with the quotient.

For example, if we were to divide 120 \div 6,

How to divide using long division

In order to divide using long division, first identify the dividend and divisor. You will write the dividend under a division bracket, with the divisor to the left.

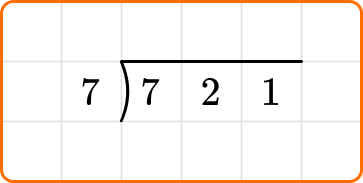
You will then start a sequence of steps that include dividing, multiplying and subtraction. These steps can be done once, or many times, depending on the size of the divisor and dividend.

Divide : First, calculate how many times the divisor 7 can divide into the first digit of the dividend, 7.

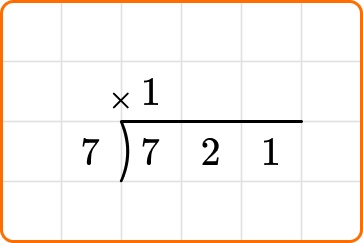
Multiply : The 1 will be placed above the top line of the division bracket, and multiplied by the divisor, 7.

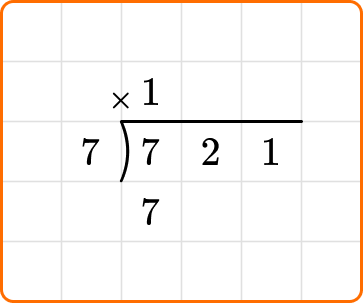
Subtract : Place this number under the first number in the hundreds place, 7 and subtract.

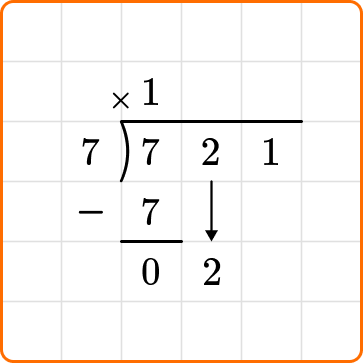
Bring down the next number from the dividend, and continue dividing until all numbers in the dividend have been brought down.

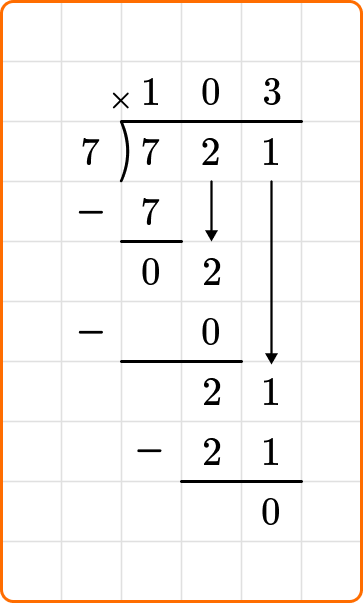
Quotients with remainders

Sometimes the dividend cannot be equally divided into by the divisor. When this happens, you would be left with a remainder. You may see a remainder in different formats:

• As a whole number
• As a decimal
• As a fraction

Students in upper grade levels are often taught to leave the reminders as either whole numbers or fractions. As students move into long division in middle school, students will be expected to express their remainders as fractions.

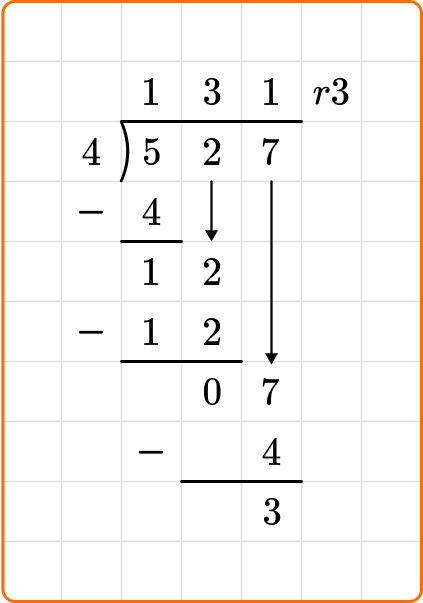
If you divide 527 \div 4, you will end up with a remainder of 3. Let’s look at how you can show the remainder of 3 in all three ways:

Remainders as a whole number

When you leave the remainder as a whole number, you will write a lowercase r to the right of the quotient, and place the remainder after.

For example,

Remainders as a fraction

When you leave your remainder as a fraction, you will write the remainder as the numerator, and the divisor as the denominator.

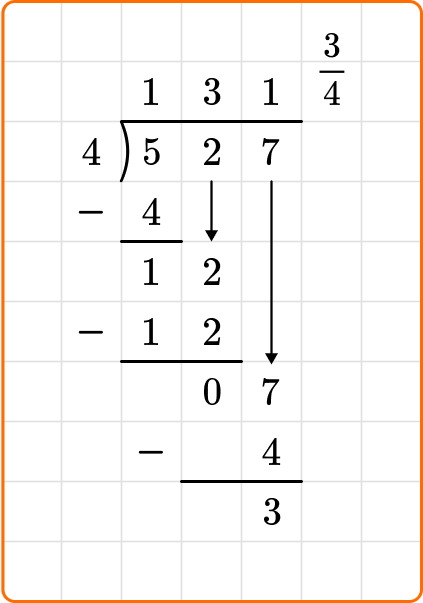
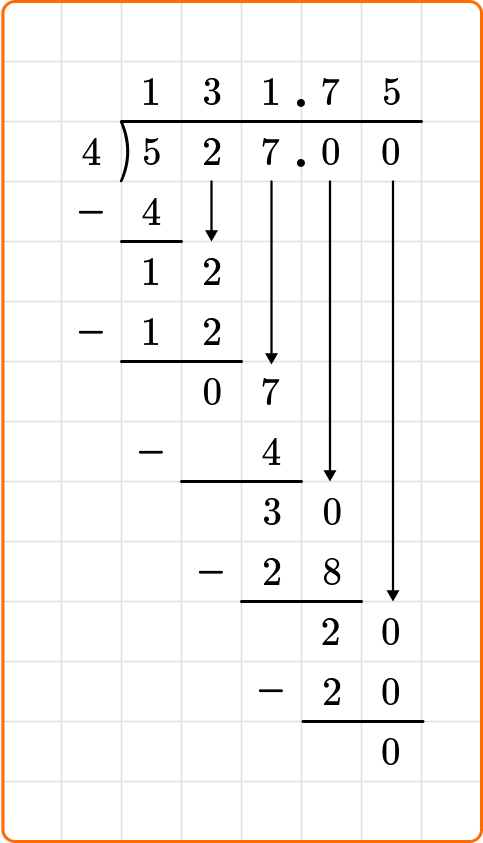
Remainder as a decimal

When asked to leave your remainder as a decimal, you will continue dividing. First, you will place a decimal to the left of the ones place of the dividend, as well as in the quotient. After the decimal place next to the dividend, place a zero.

You will then bring that zero down, as you had all the digits from the dividend, and continue dividing until you get a remainder of zero.

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

• Grade 6 – The Number System (6.NS.B.2) Fluently divide multi-digit numbers using the standard algorithm.
• Grade 7 – The Number System (7.NS.A.2d) Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.

[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)

Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4th, 5th and 7th grade multiplication and division topics to identify areas of strength and support!

In order to divide using long division, you need to:

Set up the division equation using a division bracket.

Divide, multiply and subtract.

Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.

State your answer.

Long division examples

Example 1: long division without remainders.

Solve 672 \div 6.

Write the dividend, 672, inside the division bracket, and the divisor, 6, out to the left of the division bracket.

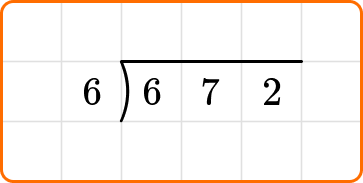
2 Divide, multiply and subtract.

Ask yourself: How many times does 6 go into the first digit of the dividend 6?

Divide: 6 \div 6=1

Write the number 1 above the long division symbol.

Multiply: 6 \times 1=6

Write the result beneath the dividend.

Subtract: 6-6=0

Bring down the next digit of the dividend, the 7.

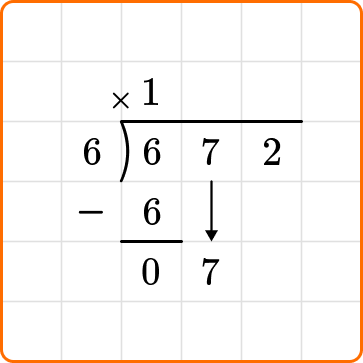
3 Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.

Ask yourself: How many times does 6 go into 7?

Divide: 7 \div 6=1

Subtract: 7-6=1

Bring down the next digit of the dividend, 2, beside the 1.

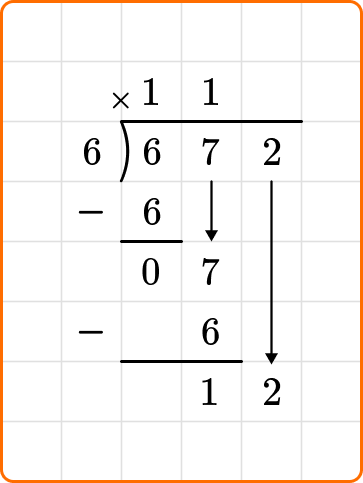
12 is larger than the divisor 6, so continue dividing.

Ask yourself: How many times does 6 go into 12?

Divide: 12 \div 6=2

Write the number 2 above the long division symbol.

Multiply: 6 \times 2=12

Subtract: 12-12=0

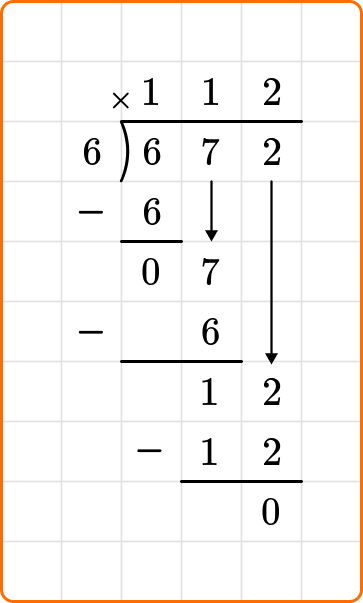
There is no remaining value to divide, so you are done dividing. The quotient is the number on the top of the division bracket.

4 State your answer.

Example 2: long division without remainders

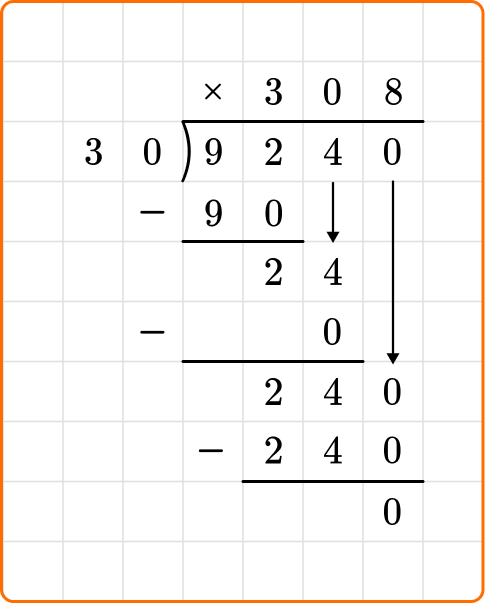
Solve 9,240 \div 30.

Write the dividend, 9,240, inside the division bracket, and the divisor, 30, out to the left of the division bracket.

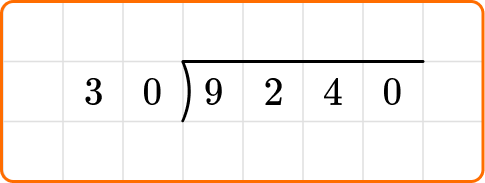
Ask yourself: How many times can 30 go into 92?

Divide: 92 \div 30=3

Write the number 3 above the long division symbol.

Multiply: 30 \times 3=90

Subtract: 92-90=2

Bring down the next digit of the dividend, 4, beside the 2.

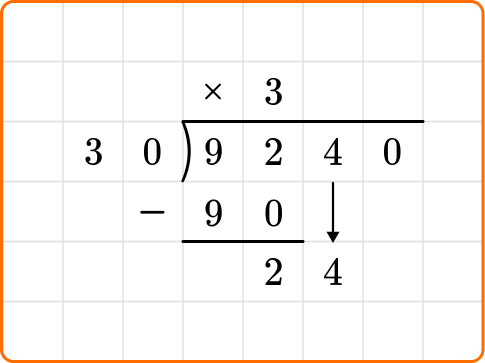
Ask yourself: How many times does 30 go into 24?

Divide: 24 \div 30=0

Write the number 0 above the long division symbol.

Multiply: 30 \times 0=0

Subtract: 24-0=24

Bring down the remaining dividend, 0, and you are left with 240.

240 is larger than the divisor 30, so continue dividing.

Ask yourself: How many times 30 goes into 240?

Divide: 240 \div 30=8

Write the number 8 above the long division symbol.

Multiply: 30 \times 8=240

Subtract: 240-240=0

Example 3: long division with whole number remainders

Solve 763 \div 28. Write the remainder as a whole number.

Write the dividend, 763, inside the division bracket, and the divisor, 28, out to the left of the division bracket.

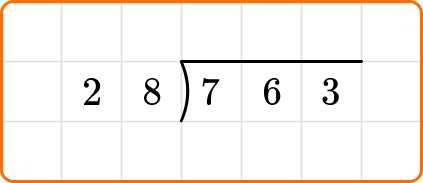
Ask yourself: How many times does 28 go into the first two digits of the dividend, 76?

Divide: 76 \div 28=2

Multiply: 28 \times 2=56

Subtract: 76-56=20

Bring down the next digit of the dividend, the 3.

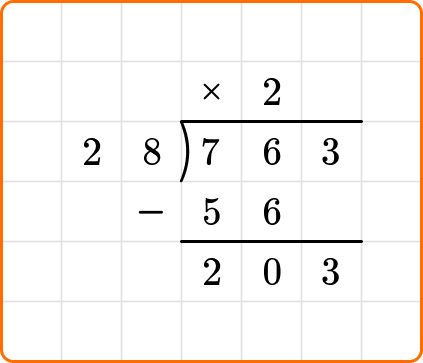
Ask yourself: How many times does 28 go into 203?

Divide: 203 \div 28=7

Write the number 7 above the long division symbol.

Multiply: 28 \times 7=196

Subtract: 203-196=7

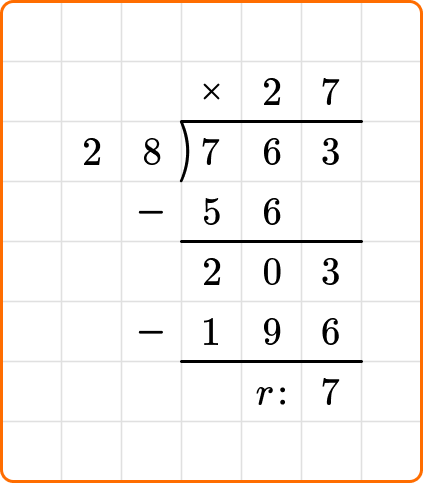
7 is less than the divisor 28, so you are finished dividing.

The question states to write your remainder as a whole number.

763 \div 28=27 \; r7

Example 4: long division with remainders as fractions

Solve 167 \div 8. Write your remainder as a fraction.

Write the dividend, 167, inside the division bracket, and the divisor, 8, out to the left of the division bracket.

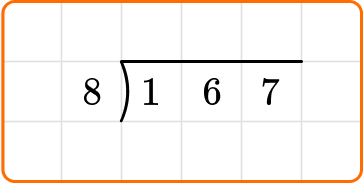
Ask yourself: How many times does 8 go into the first two digits of the dividend, 16?

Divide: 16 \div 8=2

Multiply: 8 \times 2=16

Subtract: 16-16=0

Bring down the next digit of the dividend, 7, beside the 0.

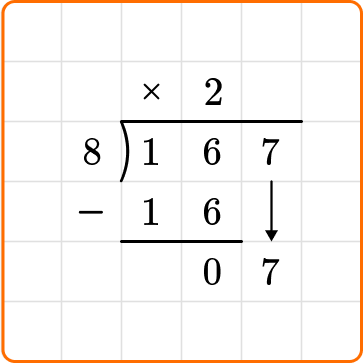
Ask yourself: How many times does 8 go into 7?

Divide: 7 \div 8=0

Multiply: 0 \times 8=0

Subtract: 7-0=7

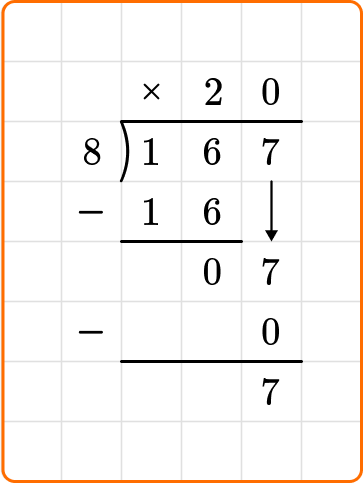
7 is less than 8, so you are done dividing.

To write your remainder as a fraction, the remainder is the numerator and the divisor becomes your denominator.

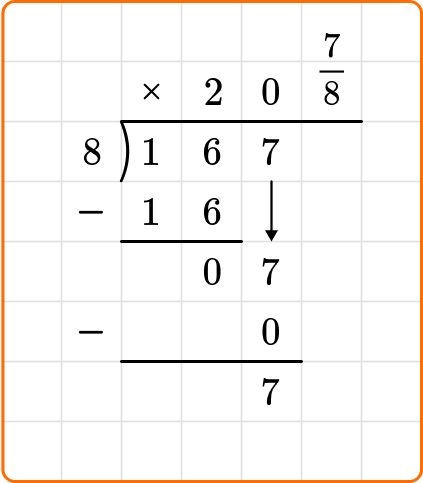
The question states to write your remainder as a fraction.

167 \div 8=20 \cfrac{7}{8}

Example 5: long division with a decimal remainder

Solve 53 \div 4. Write your remainder as a decimal.

Write the dividend, 53, inside the division bracket, and the divisor, 4, out to the left of the division bracket.

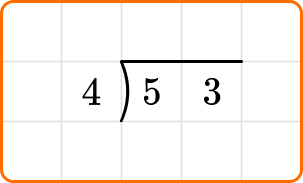
Ask yourself: How many times does 4 go into the first digit of the dividend, 5?

Divide: 5 \div 4=1

Multiply: 4 \times 1=4

Subtract: 5-4=1

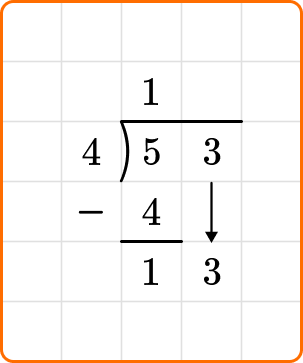
Ask yourself: How many times does 4 go into 13?

Divide: 13 \div 4=3

Multiply: 4 \times 3=12

Subtract: 13-12=1

Because the problem states to write the remainder as a decimal, you will keep dividing, even though the remainder is less than the divisor.

You will add a decimal point after the 3 in 53, followed by a 0. Make sure to write the decimal point above the division bracket too. Bring the zero down next to the 1 and continue dividing.

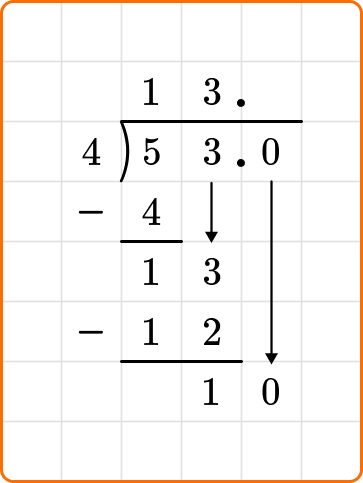
Ask yourself: How many times does 4 go into 10?

Divide: 10 \div 4=2

Write the number 2 above the division symbol, to the right of the decimal point.

Multiply: 4 \times 2=8

Subtract: 10-8=2

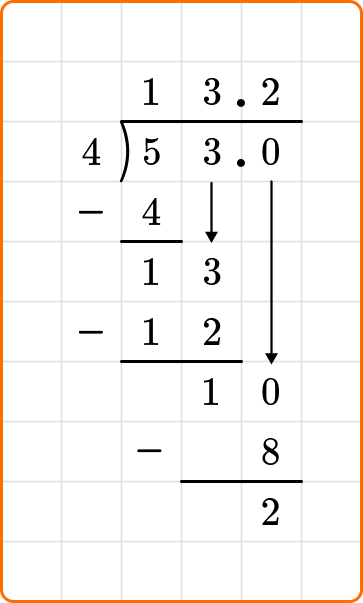
You will repeat the process of adding another zero to the dividend and bring it down until you have a zero after subtracting.

Ask yourself: How many times does 4 go into 20?

Divide: 20 \div 4=5

Write the number 5 above the long division symbol.

Multiply: 4 \times 5=20

Subtract: 20-20=0

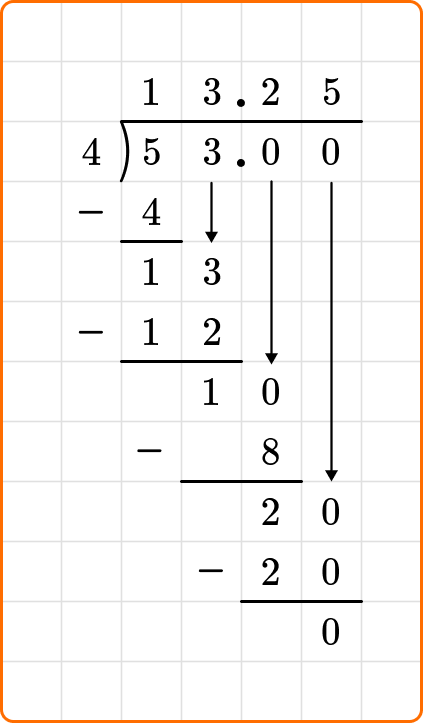
The problem states to write your remainder as a decimal.

53 \div 4=13.25

Example 6: long division word problem

Cassie received \$1,260 for her graduation. She wants to spend the money equally over the next 6 months. How much money can Cassie spend each month?

Write the dividend, 1,260, inside the division bracket, and the divisor, 6, out to the left of the division bracket.

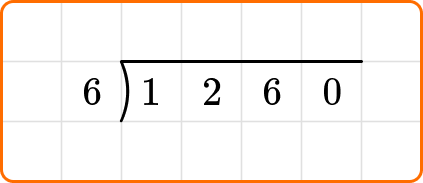
Bring down the next digit of the dividend, the 6.

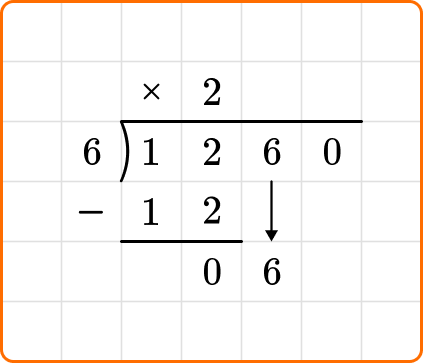
Ask yourself: How many times does 6 go into 6?

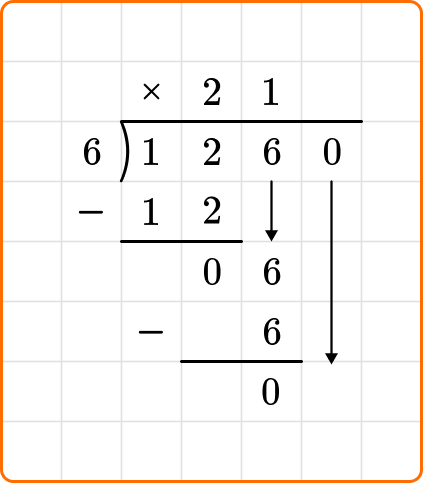
Ask yourself: How many times does 6 go into 0?

Divide: 6 \div 0=0

Multiply: 6 \times 0=0

Subtract: 0-0=0

Cassie can spend \$210 each month.

1260 \div 6=210

Teaching tips for long division

• Make sure students have a firm grasp on how to divide using partial quotients, as it helps students visualize why the long division method works.
• If using long division worksheets, start with simple long division problems, such as dividing by one digit divisors with no remainders. Once students begin grasping the concept of long division, increase the challenge of the problems, including large numbers.
• Emphasize paying attention to the place value of each digit as they set up and solve the problem. Allowing students to use graph paper when first beginning long division will allow them to easily organize their math, especially when working with larger numbers.
• Providing the students with step-by-step division steps allows them to refer back to them as needed. These can be displayed within the classroom on an anchor chart or in their math journals.
• Allow students to check their answers using a long division calculator. This allows real time feedback for students so they do not continue to practice the long division algorithm incorrectly.

Easy mistakes to make

• Forgetting to bring down the next number Students will divide the first set of numbers correctly but may forget they need to bring down the next digit from the dividend to continue dividing. Having an example of a complete long division problem will give students something to refer back to.
• Alignment issues Proper placement of numbers is important and can lead to calculation errors if the work is not organized. Allowing students to use graph paper is one way to assist with this.

Related multiplication and division lessons

• Negative numbers
• Negative times negative
• Multiplying and dividing integers
• Multiplying and dividing rational numbers
• Multiplying multi digit numbers
• Multiplicative comparison
• Dividing multi digit numbers
• Multiplication

Practice long division questions

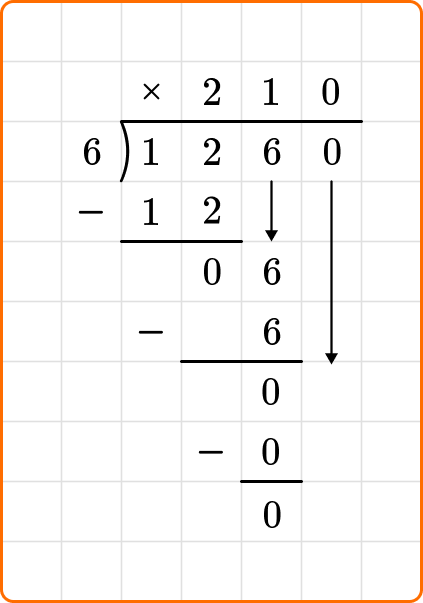
1. Solve 528 \div 16.

Set up your division equation with the dividend, 528, inside the division bracket and the divisor, 16, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 16.

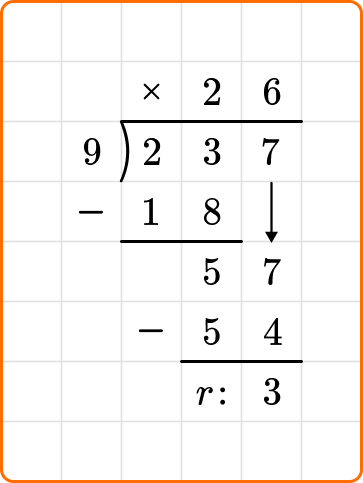
2. Divide 237 \div 9.

Set up your division equation with the dividend, 237, inside the division bracket and the divisor, 9, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 9.

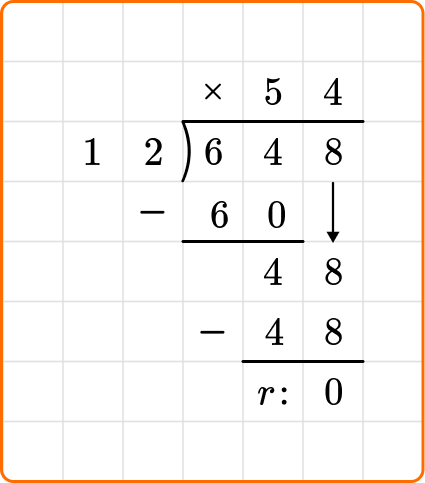
3. Solve 648 \div 12.

Set up your division equation with the dividend, 648, inside the division bracket and the divisor, 12, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 12.

4. Solve 489 \div 15. Write the quotient as a decimal.

Set up your division equation with the dividend, 489, inside the division bracket and the divisor, 15, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a decimal.

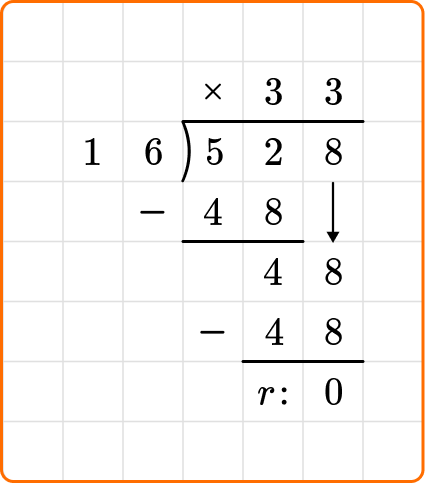
5. Solve 357 \div 8. Write the quotient as a fraction.

Set up your division equation with the dividend, 357, inside the division bracket and the divisor, 8, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a fraction.

6. Mrs. Davis had 112 pencils to divide into 9 pencil boxes. How many pencils did Mrs. Davis put in each pencil box?

Set up your division equation with the dividend, 112, inside the division bracket and the divisor, 9, to the left.

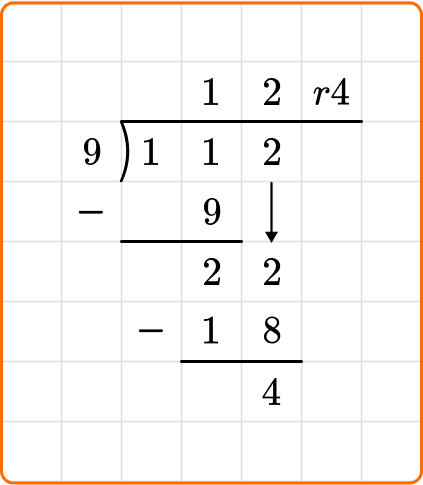
Mrs. Davis can equally place 12 pencils in each pencil box and will have 4 pencils left over.

Long division FAQs

The number of decimal places will vary by division problem. Some division problems will only have one decimal place, while others will have many.

The long division symbol is sometimes called a division bracket, but does not have an established name.

The next lessons are

• Types of numbers
• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

Long Division - Introduction

John and Ann are given $10 to share. How do they share it? Easy! $5 each.

But then they think of their little baby brother Max.

"Maybe we should share it with him?" they ask each other.

So how much do they each get?

$10 shared amongst 3 people

That is $3 each ... but 3 lots of $3 is $9:

That leaves $1 still to share.

Let us break that $1 into ten 10c pieces:

OK. Let's share those 10 cent pieces. That is an extra 30 cents each:

But that still leaves 10c !!!

So let us turn the 10c into ten 1c pieces:

OK, share that too: they each get 3c more:

That leaves one cent! But we can't break that cent any further so it is simply "left over", which we call the " remainder "

The answer is: they each get $3 and another 30c and another 3c for a totsl of $3.33 each, with one cent left over!

$3.33 each (with a remainder of 1c)

That is how Long Division works!

In Long Division we:

• do the best division we can,
• then find out what is left over, and try to divide that,
• around and around until we can't go any further!

It is Written Down in a Special Way

First, we write down that we want to divide $10 by 3 like this:

Note: We don't use the $ symbol, instead we write the $10 as the number 10.00 meaning 10 dollars and 0 cents

Then we write down that we took 3 lots of $3 to make $9:

We write the 9 below the 10, because the next thing to do is to subtract $9 from $10 to find we still have $1 left to divide:

Next is to repeat the whole thing , but do it for the $1 (which is written as 1.00):

That leaves 10 cents, or 0.10 yet to divide, so we repeat again :

We can't divide any more, so that is our answer!

$10 divided by 3 is $3.33 with $0.01 (1 cent) remainder

Now have a look at this Long Division Animation

We use cookies to enhance our website for you. Proceed if you agree to this policy or learn more about it.

• Essay Database >
• Essays Examples >
• Essay Topics

Essays on Long Division

1 sample on this topic

Our essay writing service presents to you an open-access database of free Long Division essay samples. We'd like to stress that the showcased papers were crafted by proficient writers with relevant academic backgrounds and cover most various Long Division essay topics. Remarkably, any Long Division paper you'd find here could serve as a great source of inspiration, actionable insights, and content structuring practices.

It might so happen that you're too pressed for time and cannot allow yourself to spend another minute browsing Long Division essays and other samples. In such a case, our service can offer a time-saving and very practical alternative solution: a completely original Long Division essay example written particularly for you according to the provided instructions. Get in touch today to know more about efficient assistance opportunities provided by our buy an essay service in Long Division writing!